7 minutes
Talking about Big O Notation
Hello everyone !
After few week ago break to writing a blog and trying to re-learn about Data Structures and Algorithms, here I would like to share one thing that I think is important to how analysis performance some algorithms, ya Big-O notation (read with an O, not a zero). Honestly, there are so many method to analyze performance some algorithm, but here I only share the most method that we usually use to analyze an algorithm. We often use Big-O notation as a simple way to describe the speed or approximate run time of an algorithm, that’s why we always should be taking Big-O to consideration when we are writing algorithm.
Actually, I write this blog is based on books that I am read recently, “Data Structure and Algorithms” by Hemant Jain. You can choose another language, because I am currently having develop with Ruby, so I choose Ruby for a programming language.
Before we jump into concept of Big-O Notation, we have to ensure “what is an Algorithms” itself. From the books is :
“algorithm is a set of steps to accomplish as task or an algorithm in a computer program in which a set of steps applied over a set of input to produce a set of output”.
Simply put, it is a set of instructions for completing some task. Data structure is just some ways to store information in computer and algorithms use to manipulate the data.
Anyway, there are most important properties before we are writing an algorithm is:
- Correctness – its means when you are trying to solve problem with algorithm please make sure that the algorithm is correct and able to process all given input and provide correct output.
- Efficiency – its means the algorithm should be efficient to solve problems. Efficiency measured in two parameters, first is Time-Complexity and second is Space-Complexity.
Time-Complexity is every or each algorithm certain needed of time to run or complete to provided the result or in other words how to quick result provided by the algorithm.
Space-Complexity is how much additional memory or storage of your algorithm consume to give the result. But here, I make boundaries in this article that we just discuss about Time-Complexity.
So, what is exactly Big-O notations? Big-O is used to describe performance of an algorithm, or in other words we use Big-O to measured how efficient our algorithm run that represent time complexity. We use it as a tool to compare algorithm to other algorithm.
For more details, you can see the graph below. The graph will be explain relationship between time and input size.
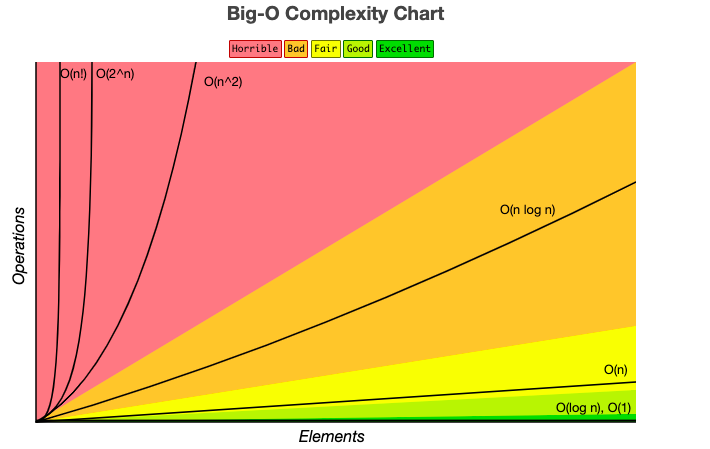
source: Big O Cheat Sheet.
As you can see, there are two main things to calculating the Big-O of an algorithms, number of operations (complexity or time) and number of input size. I sure that you wondering what is relationship between them (time and input). Actually, to find out best algorithm it’s depends on the input size. We want to keep our time or operations as low as possible also to be as efficient as possible while the size of our data increases. It’s important to avoid red zone if possible.
There are common time complexities, from fastest to slowest.
| Notation | Complexity | Rate of growth |
|---|---|---|
| O(1) | Constant | Fast |
| O(log n) | Logarithmic | |
| O(n) | Linear | |
| O(n log n) | Log Linear | |
| O(n²) | Quadratic | Slow |
Lets break down about the different notations of Big-O one by one and all examples are write in ruby.
Constant Time: O(1)
An algorithm that given input of n size and only takes a single step for the algorithm. That’s why called constant, because the algorithm will always run at a constant time.
For examples
- If we want to accessing x element of an array, the run time will be constant or O(1).
- Push and pop of a stack.
- Accessing an element of Hash-Table or Dictionary.
def show_array(arr)
puts “#{arr[0]}”
end
arr = [2,4,5,7,9,10,12]
show_array(arr)
The reason the runtime of this method is O(1) is no matter how big the array, the number of operations doesn’t change.
Logarithmic Time: O(log n)
An algorithm that given an input of size n, the number of steps it takes to accomplish the task are decreased by some factor with each step.
The most common example that used logarithmic time is binary search. Basically, binary search is an algorithm to search some position in an array by elimination a half of input array to find out the position. We have to make sure that the array input have sorted before. Actually, to understand the binary search we have to know the concept of recursive function.
Lets take a look the example below for binary search.
def search(arr, target)
search_rekursif(arr, 0, arr.length-1, target )
end
def search_rekursif(arr, low, high, target)
if low > high
return print 'Cannot find the target'
end
mid = low +(high-low)/2
if arr[mid] == target
return print mid
elsif arr[mid] < target
return search_rekursif(arr, mid +1, high, target)
else
return search_rekursif(arr, low, mid-1, target)
end
end
arr = [2,4,5,7,9,10,12]
target = 4
search(arr,target)
As you can see, we will find where the position of the target with return location on the arrays input. We start in the function search that will be call function search_recursive.
First, we have to ensure the middle of the array, and than we compare middle value with target value, will be greater or smaller than the middle value. The middle will be minus one if the target value is smaller than middle value, that’s means the target value in the range middle to down. Otherwise, the middle will be plus one if the target is greater than middle value. This is done until match is found.
Linear Time: O(n)
An algorithm is said to run in linear time if the execution time of the algorithm is directly proportional to the input size.
def show_all(items)
items.each do |item|
print item
end
end
As you can see, we have to see/traverse all items one by one to print out all items. An array with size lets say 10, so the method will be take 10 iterations, so as an input increases, runtime will be also increases.
LogLinear: O(n log n)
An algorithm is said to run in logarithmic time if the execution time of an algorithm is proportional to the product of input size and logarithm of the input size.
Actually, good example to log linear is a quicksort algorithm. But talk this algorithm is different part. I only give a example to imagine loglinear, if you have 10 size or array than you want to sorting, the time complexity only 20 time complexity. Sounds good but quicksort is special kind of algorithm, quicksort will be O(n log n) with average case but with worse case will be O(n²).
Quadratic Runtime: O(n²)
An algorithm that given input of size n, the number of steps it takes to accomplish a task is square of n.
Bubble sort, selection sort and insertion sort is examples for O(n²).
def print_all(arrays)
arrays.each do |array_1|
arrays.each do |array_2|
print "#{array_1}" + "#{array_2}"
end
end
end
arrays = [1,2,3]
print_all(arr)
As you can see, there is have loop inside loop or a nested loop. You can imagine if size of input let say 10 and will take 100 iteration. That’s why called exponential runtime because the loop has to square the amount of iteration based on the input size. That it.
Well, with understand of concept Big-O notation we will easily to looks which one is the best? and which one is more efficient to solve problems?
I would like to thank you for reading. I hope you have learned something new or this post can help you to introduce what is Big-O.
Thank you !!!